A/B testen worden steeds vaker gebruikt om te bepalen wat wel en niet werkt voor je webshop. Niet elke test is levert direct rendement op, dat is logisch. Des te groter de blijdschap als er wel een positief significant verschil wordt gemeten in een A/B test. Maar is dat significante verschil wel waar? Hoe vaak zijn jouw winnende testen eigenlijk echte winnaars?

Welke significantiegrens hanteer je?

In een A/B test toets je hoe groot de kans er is dat het gemeten verschil kan zijn ontstaan door toeval. Je bepaalt vooraf wanneer je het risico op toeval accepteert. Een normaal uitgangspunt voor veel organisaties is een P-waarde (de waarschijnlijkheidswaarde) van 0,1. Dit vertaalt zich naar een significantiegrens van 90%. Een A/B testuitslag waarbij het verschil ten faveure van de nieuwe versie dan 90% significant of meer is, wordt dan gezien als een positief significant resultaat.

Hiermee wordt het risico geaccepteerd dat in 1 van de 10 A/B-testen zonder effect in de werkelijkheid er toch een positief significant verschil gemeten wordt. Werken met een hogere significantiegrens wordt vaak vermeden om te voorkomen dat de kans op het vinden van winnaars erg klein wordt (er zijn dan veel meer bezoekers en conversies nodig).

Met welke Power toets je?

Power geeft aan hoe groot de kans is om in een A/B test een significant resultaat te meten bij een bepaalde significantiegrens, wanneer er in werkelijkheid inderdaad een verschil is. Hoe kleiner het verschil is dat je wilt kunnen detecteren, hoe meer bezoekers en conversies er nodig zijn in de A/B test. Te weinig Power in A/B testen zorgt er vaak voor dat verschillen die er in werkelijkheid wel zijn, niet gemeten kunnen worden. De meeste organisaties werken met een Power van 80%. Zij willen dat in 80% van de A/B testen waarin er in werkelijkheid een winnaar is ook daadwerkelijk een positief significant resultaat uit de A/B-test komt.

Gemeten winnaars vs. echte winnaars

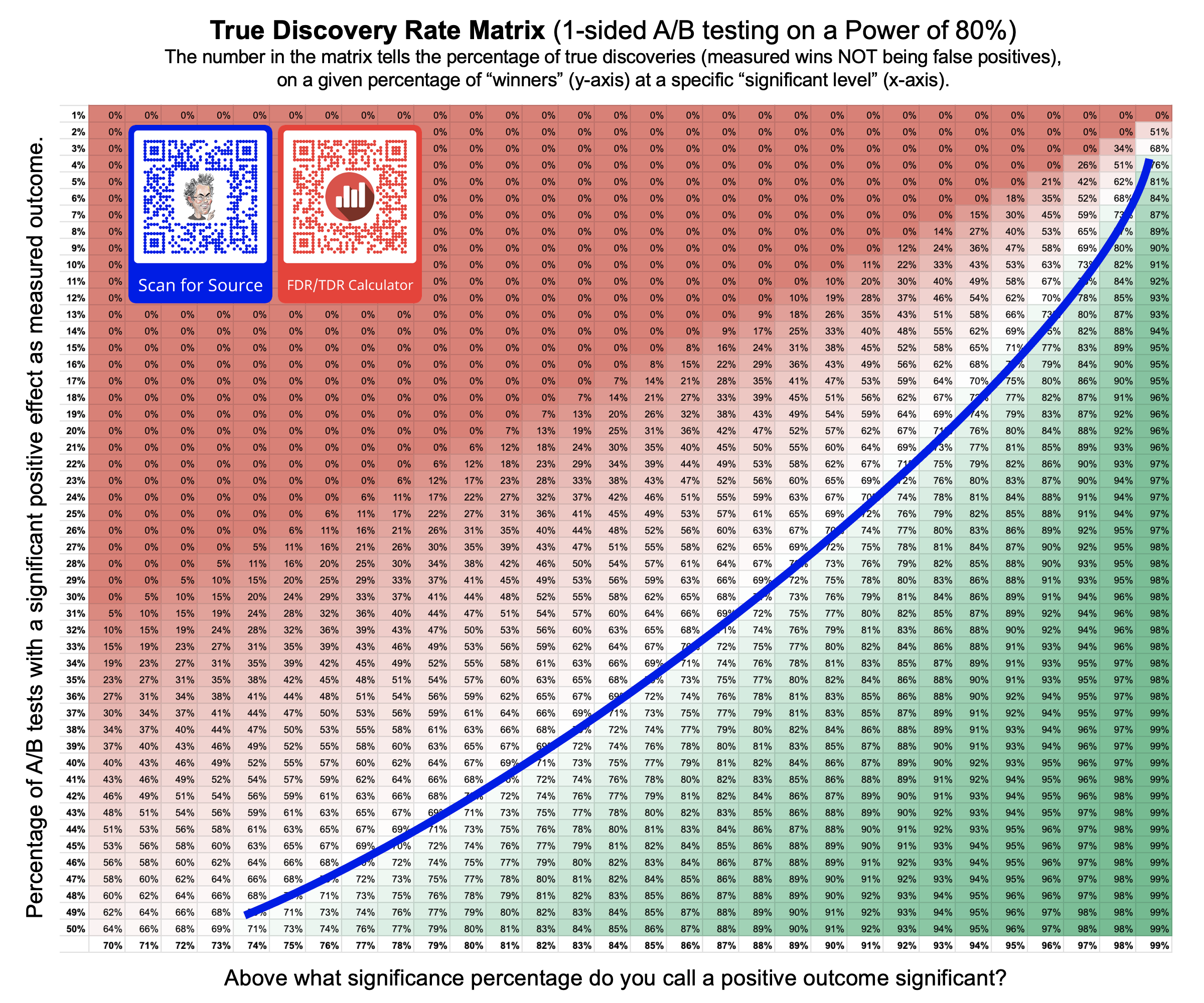
Uit eerder onderzoek blijkt dat organisaties gemiddeld 25% significante positieve resultaten meten in hun A/B testen: 100 A/B testen = 25 gemeten winnaars. Met de gangbare Power van 80% en de significatiegrens van 90% kun je uitrekenen hoeveel van deze winnaars echte winnaars zijn (en niet een vals positief resultaat). In dit voorbeeld is dat 69%. Dit is op het randje van acceptabel. Ruim 3 op de 10 winnaars zijn geen echte winnaars. Iets om bij stil te staan voordat je conclusies uit hypotheses trekt!

Soms werken organisaties met een significatiegrens van 80%, omdat dit fijn veel extra gemeten winnaars oplevert. Niet 25%, maar bijvoorbeeld 32%. Het aantal echte winnaar daalt in dit voorbeeld echter naar 50% en dat is zodanig veel dat zelfs je absoluut aantal echte winnaars lager is (waarbij je niet weet wat de echte winnaars onder je gemeten winnaars zijn). Blijf dit goed berekenen, voordat je keuzes maakt wel welke significatiegrens je gaat werken.

Waarheidsmatrix

Zoek jouw waarde op in de onderstaande waarheidsmatrix of gebruik deze calculator om jouw waarde te berekenen op basis van jouw (gerealiseerde) Power.