De mogelijkheden in de online wereld voor het (AB) testen van zo goed als bijna alles zijn immens. Veel experimenten worden dan ook uitgevoerd en de resultaten daarvan geïnterpreteerd op basis van de regels van nulhypothesetoetsing, “Is het effect significant?”.

Een belangrijk aspect in het dagelijkse leven van de online analist is dan ook het bepalen van de steekproefomvang bij het inrichten van tests. Hier wordt helaas erg vaak “gerommeld”.

In dit artikel wordt aan de hand van een dagelijkse case een aantal benaderingen voor steekproefgroottebepaling besproken met aandacht voor de statistische fundementals. Een les in statistiek. Ga er maar eens goed voor zitten. Dit is deel I: de uitdaging

Case:

Een marketeer heeft een alternatief bedacht voor een landingspagina; de originele landingspagina heeft een conversie van 4%, de conversieverwachting voor de alternatieve pagina is 5%. De marketeer vraagt de analist “Hoe groot moet de steekproef zijn om aan te tonen dat het alternatief statistisch significant beter scoort dan het origineel?”.

Oplossing “standaard steekproefgrootte”

De analist zegt: split run (AB test) met 5.000 waarnemingen elk en een eenzijdige toets met een betrouwbaarheid van .95. Uit gewoonte 🙂

Maar wat gebeurt er bij deze benadering?

Wat er concreet gebeurt bij het trekken van twee steekproeven voor het schatten van het verschil in proportie successen tussen beide, met een eenzijdige toets en een betrouwbaarheid van .95, kan voor deze case inzichtelijk worden gemaakt door het oneindig vaak trekken van twee steekproeven van 5.000 waarnemingen uit een populatie met een conversie van 4%, en het verschil in conversie per paar (per ‘test’) tussen beide steekproeven te plotten in een grafiek en daar vervolgens het significantiegebied in aan te geven:

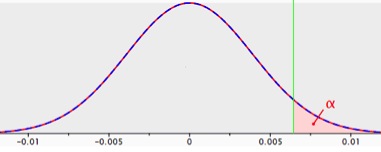
Figuur 1: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04 en n1=n2=5.000; het significantiegebied is aangegeven voor alpha=.05 (betrouwbaarheid .95) met een eenzijdige toets.

Deze grafiek geeft weer wat formeel wordt genoemd de steekproevenverdeling voor het verschil tussen twee proporties. Het is de kansverdeling voor alle mogelijke steekproefuitkomsten berekend voor het verschil tussen p1=.04 en p2=.04 bij n1=5.000 en n2=5.000. Deze verdeling is het uitgangspunt bij nulhypothesetoetsing. De nulhypothese luidt dat er geen verschil is tussen beide landingspagina’s en deze hypothese wordt vanuit deze kansverdeling getoetst op significantie.

Met p=.04 wordt bedoeld conversiekans=4%. In de statistiek wordt gesproken over proporties die kunnnen liggen tussen 0 en 1, terwijl in de dagelijkse taal meestal wordt gesproken over percentages die kunnen liggen tussen 0 en 100. Hier wordt om te conformeren aan de grafiek, gebruik gemaakt van proportienotatie met waarden tussen 0 en 1.

Deze kansverdeling kan met deze sps syntax (dertig gepaarde steekproeven uit een populatie.sps) bij ruwe benadering worden gerepliceerd. Daarmee wordt niet oneindig vaak, maar 30 keer een gepaarde steekproef getrokken met p1=.04, p2=.04 en n1=5.000, n2=5.000 en de verschilscores worden geplot in een histogram met daarin de normaalverdeling op basis van gemiddelde en standaarddeviatie (het laatste plaatje in de output). Dit geeft een beeld bij het principe van een steekproefverdeling.

De modale waarneming van het conversieverschil tussen beide groepen is nul. Logisch, beide groepen komen uit dezelfde populatie met conversie 4%. Afwijkingen ten opzichte van nul zowel naar links (origineel doet het beter) als naar rechts (alternatief doet het beter) kunnen en zullen optreden, gewoon door toeval. Hoe verder van nul, des te kleiner echter de kans van optreden. Het rechts gelegen roze gebied met het teken alpha erin is het significantiegebied van .05, ofwel de onbetrouwbaarheid=1-betrouwbaarheid=1-.95.

Valt bij een test het verschil tussen conversie alternatief en conversie origineel in het roze gebied, dan wordt de nulhypothese dat er geen verschil is tussen beide landingspagina’s verworpen ten gunste van de hypothese dat het alternatief beter scoort dan het origineel. Op de x-as is niet zoals gebruikelijk de waarde van de toestingsgrootheid weergegeven (Z in dit geval), maar voor de overzichtelijkheid het concrete verschil in conversie tussen beide landingspagina’s.

Dus wanneer de alternatieve landingspagina in een split run test meer dan 0.645% (=waarde .00645 op de x-as) beter scoort (relatief 16% beter scoort ten opzichte van 4%) dan de originele landingspagina (en daarmee in het significantiegebied terecht komt), wordt de nulhypothese dat er geen verschil in conversie is tussen de landingspagina’s verworpen ten gunste van de hypothese dat het alternatief het beter doet dan het origineel. Voor de volledigheid, dit percentage correspondeert met de waarde 1.65 van toetsingsgrootheid Z.

Voordeel van deze werkwijze is dat door te kiezen voor een vaste steekproefomvang impliciet een zekere standaardisatie is ingebracht. Verschillende tests zijn wat dat betreft vergelijkbaar.

Nadeel bij deze benadering is dat wel bekend is wat de kans is de nulhypothese te verwerpen wanneer deze waar is -een onjuiste beslissing-, namelijk de zelf gekozen alpha van .05, maar niet wat de kans is de nulhypothese niet te verwerpen wanneer deze niet waar is: de kans dat het alternatief feitelijk (op populatieniveau) beter scoort dan het origineel, maar dat dit door toeval niet als statistisch significant uit de bus kom; ook een onjuiste beslissing. De kans de nulhypothese niet te verwerpen wanneer deze niet waar is, wordt beta genoemd. 1-beta is daarmee de kans de nulhypothese wel te verwerpen wanneer deze niet waar is –een juiste beslissing-. Dit wordt onderscheidingvermogen genoemd, of power.

Voor de overzichtelijkheid de terminologie nog op een rijtje

alpha = onbetrouwbaarheid = de kans de nulhypothese te verwerpen wanneer de nulhypothese feitelijk waar is. Dit is een foute beslissing. De nulhypothese had niet verworpen moeten worden.

1-alpha = betrouwbaarheid = de kans de nulhypothese niet te verwerpen wanneer deze waar is. Een correcte beslissing. De nulhypothese is terecht niet verworpen.

beta = de kans de nulhypothese niet te verwerpen wanneer deze feitelijk niet waar is. Een foute beslissing. De nulhypothese had wel verworpen moeten worden.

1-beta = power = de kans de nulhypothese te verwerpen wanneer deze niet waar is. Een correcte beslissing. De nulhypothese is terecht verworpen.

Power is een functie van alpha, steekproefomvang en effect (het effect in deze is het werkelijke verschil in conversie tussen de beide landingspagina’s, lees, op populatieniveau de toegevoegde waarde in conversiepercentage van de alternatieve site ten opzichte van de originele site). Hoe kleiner alpha, steekproefomvang of effect, des te kleiner de power.

Alpha stelt de onderzoeker zelf in -in dit voorbeeld .05-, de steekproefomvang ook, 5.000 voor origineel, 5.000 voor alternatief, rest het effect. En het werkelijke effect is per definitie onbekend. Echter is het niet onrealistisch om daar commerciële targets of ervaringsgetallen voor te gebruiken. Zoals in de voorbeeldcase door de marketeer is geformuleerd: een verwachte verbetering van 4% naar 5%. Als dat werkelijk waar is, wil marketeer dat met gerede kans ook als statistisch significant in een test terugvinden.

Een voorbeeld om dit inzichtelijk te maken en het belang van power te verduidelijken: stel dat de werkelijke (=populatie)conversie van het alternatief inderdaad 5% is. De steekproevenverdeling voor het verschil tussen twee proporties met conversie1=4%, conversie2=5% en n1=n2=5.000, wordt geplot naast de eerder gemaakte steekproevenverdeling met conversie1=conversie2=4% en n1=n2=5.000.

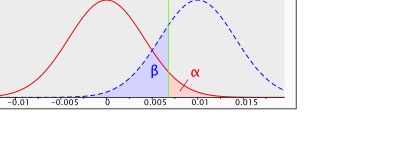
Figuur 2: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04, n1=n2=5.000 (rode lijn) en p1=.04, p2=.05, n1=n2=5.000 (onderbroken blauwe lijn), met een betrouwbaarheid van .95 en een eenzijdige toets.

De onderbroken blauwe lijn toont de steekproevenverdeling van het verschil in conversiepercentages tussen origineel en alternatief wanneer in wekelijkheid (op populatieniveau) het origineel 4% en het alternatief 5% scoort. De verdeling onder de nulhypothese, de rode lijn, is in principe naar rechts verschoven. De modale waarneming van deze nieuwe verdeling met het veronderstelde effect van 1% is uiteraard 1%. Met weer steekproeftoevaltreffers naar rechts en naar links.

Alle waarnemingen rechts van de groene lijn (de markering van het significantiegebied) worden als significant beschouwd. Alle waarnemingen links van de groene lijn worden als niet significant beschouwd. Het gebied onder de ‘blauwe’ verdeling links van de significantielijn is ‘beta’, de kans de nulhypothese niet te verwerpen wanneer de nulhypothese niet waar is, en beslaat bij narekening 22% van de totale blauwe verdeling.

Het gebied onder de blauwe verdeling rechts van de significantielijn is de power, en beslaat 78% van de totale blauwe verdeling, het complement van beta. Wanneer het effect feitelijk 1% is (een relatieve conversieverbetering van 25% ten opzichte van het origineel), is de kans dat dit als significant uit de bus komt in een test met n1=5.000, n2=5.000, .78 (power). Misschien acceptabel, misschien niet, dat is afhankelijk van de mening van marketeer en de analist.

Geen eenvoudige materie, maar wel van belang. Stel dat de verwachting dat de conversietoename ten opzichte van het origineel 10% bedraagt realistisch en commercieel interessant is: 4,0% origineel vs 4,4% voor het alternatief. Dan ziet het plaatje er als volgt uit:

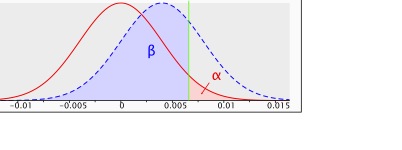
Figuur 3: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.040, n1=n2=5.000 (rode lijn) en p1=.040, p2=.044, n1=n2=5.000 (onderbroken blauwe lijn), met een betrouwbaarheid van .95 en een eenzijdige toets.

De power is nu .26. Als het van groot belang is het veronderstelde effect van 4,0% origineel vs 4,4% voor het alternatief met gerede kans, bijvoorbeeld .95, als significant terug te vinden in een test, heeft deze testopzet niet veel zin, lees is contraproductief, omdat de kans slechts .26 is dat de test zal leiden tot een significant resultaat, terwijl het effect wel degelijk bestaat.

Bovenstaande plaatjes zijn vervaardigd met het programma Gpower.

Dit programma biedt voor een groot aantal typen tests de mogelijkheid power te berekenen uit gewenste alpha, steekproefomvang en verondersteld effect. Ook kan benodigde steekproefomvang berekend worden uit gewenste power, alpha en verwacht effect, benodigde alpha berekend worden uit gewenste power, steekproefomvang en verwacht effect en benodigd effect berekend worden uit gewenste power, alpha en steekproefomvang.

Als het van groot belang is het veronderstelde effect van 4,0% origineel vs 4,4% voor het alternatief met een redelijke kans, bijvoorbeeld .95, als significant terug te vinden in de test, adviseert Gpower twee steekproeven van 54.428 waarnemingen elk.

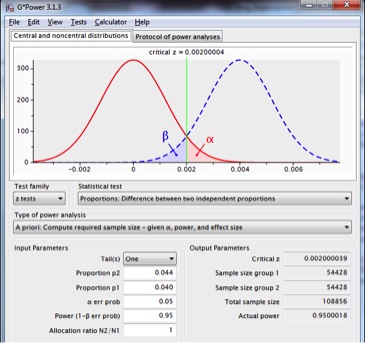
Figuur 4: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.040 (rode lijn) en p1=.040, p2=.044 (onderbroken blauwe lijn), met een betrouwbaarheid van .95, een power van .95 en een eenzijdige toets.

Dit plaatje toont informatie die bij eerdere grafieken is weggelaten en geeft daarmee ook een indruk van de interface van het programma.

Belangrijk bij deze analyses is de vraag wat de consequenties zijn van het ten onrechte verwerpen van de nulhypothese; bijvoorbeeld als op basis van een test een kostbare campagne wordt uitgerold in de veronderstelling dat het een succes zal worden en dat succes blijft uit. Ook is de vraag wat de consequenties zijn van het ten onterechte niet verwerpen van de nulhypothese, bijvoorbeeld als op basis van een test een feitelijk succesvolle campagne niet wordt uitgerold in de veronderstelling dat het geen succes zal worden.

Binnenkort volgt deel II van dit artikel: mogelijke oplossingen voor deze uitdaging.