Dit artikel over steekproeven is een vervolg op het artikel “Hoe groot moet de steekproef zijn? Deel I: de uitdaging“. Nu helder geworden is wat de problemen zijn met steekproeven, wordt het tijd voor oplossingen. Als basis wordt nog steeds dezelfde case aangehouden:

Case:

Een marketeer heeft een alternatief bedacht voor een landingspagina -de originele landingspagina heeft een conversie van 4%, de conversieverwachting voor de alternatieve pagina is 5%-. De marketeer vraagt de analist “Hoe groot moet de steekproef zijn om aan te tonen dat het alternatief statistisch significant beter scoort dan het origineel?”.

Oplossing “standaard aantal conversies”

De analist zegt tegen de marketeer: split run (AB test) met minimaal 100 conversies per testvariant en een eenzijdige toets met een betrouwbaarheid van .95.

Dit betekent in de voorbeeldcase met verwachting conversie originele pagina 4% en alternatieve pagina 5%, per testvariant 2.500 waarnemingen.

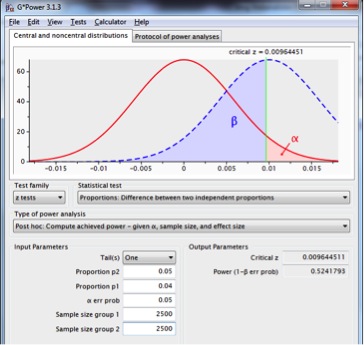
Uitgaande van dit scenario heeft deze test een power van iets meer dan .5.

Figuur 5: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04, n1=n2=2.500 (rode lijn) en p1=.04, p2=.05, n1=n2=2.500 (onderbroken blauwe lijn), met een betrouwbaarheid van .95 en een eenzijdige toets.

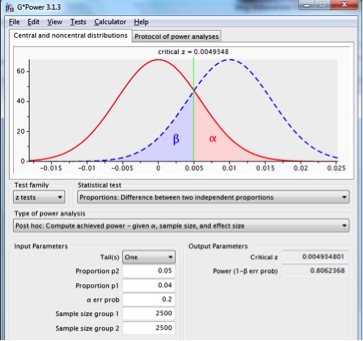
Voor een betere power zal er een groter effect aanwezig moeten zijn, de steekproefomvang groter moeten worden gekozen, of alpha worden verhoogd, bv .2:

Figuur 6: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04, n1=n2=2.500 (rode lijn) en p1=.04, p2=.05, n1=n2=2.500 (onderbroken blauwe lijn), met een betrouwbaarheid van .80 en een eenzijdige toets.

Een alpha van .2 levert een power van .8. De power is acceptabeler; de ‘kosten’ hiervoor bestaan uit een vergrote kans de nulhypothese ten onrechte te verwerpen.

Zoals gezegd zijn dit businessoverwegingen waarbij de impact van alpha en beta een sleutelrol spelen.

Benadering “standaard aantal conversies” stelt met de vuistregel op het aantal conversies feitelijk een soort grens op effectgroottes die nog zinvol (i.e met een redelijke power) te testen zijn. Ook een soort standaardisatie, en op zich geen probleem, zolang de consequenties ervan onderkend worden.

Oplossing ‘significant steekproefresultaat’:

De analist zegt: split run met zoveel waarnemingen dat indien het veronderstelde effect daadwerkelijk optreedt als testresultaat, dit significant zal zijn, bij een eenzijdige toets en een betrouwbaarheid van .95.

Dat klinkt wat raar en dat is het ook. Deze werkwijze wordt in de praktijk helaas vaak toegepast. De benodigde steekproefomvang wordt in feite teruggerekend naar het uitkomen van het veronderstelde effect in de steekproef zodanig dat dit significant is.

In het gebruikte voorbeeld: als in een test het origineel een conversie van 4% heeft en het alternatief een conversie van 5%, dan zijn er per variant minimaal 2.800 waarnemingen nodig om dit significant te laten zijn. Met bijgaande spss syntax (grens op significant steekproefresultaat.sps) kan dit worden aangetoond. Deze logica wordt toegepast bij interne afdelingsfabricaten en verschillende online berekeningtools.
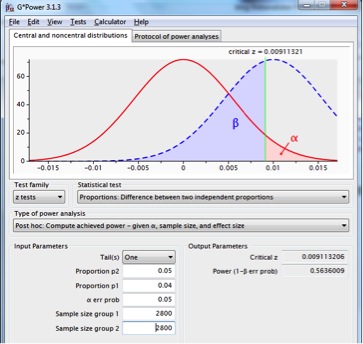
Met deze benadering wordt voorbijgegaan aan het optreden steekproeftoevalligheden –sampling error- die er toe zal leiden dat het feitelijke steekproefresultaat, gegeven het veronderstelde effect, nagenoeg even vaak kleiner als groter zal uitvallen dan de verwachtingwaarde. In principe komt dit neer op een power van .5 plus meestal een kleine extra overschrijding.

Figuur 7: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04, n1=n2=2.800 (rode lijn) en p1=.04, p2=.05, n1=n2=2.800 (onderbroken blauwe lijn), met een betrouwbaarheid van .95 en een eenzijdige toets.

Met deze werkwijze is ook een soort standaardisatie toegepast, namelijk op power, maar dat is niet de kennelijke insteek bij deze werkwijze die eerder op een misverstand lijkt te berusten.

Oplossing ‘standaard betrouwbaarheid en power’:

De analist zegt: split run met een power van .80 en een betrouwbaarheid van .95 bij een eenzijdige toets.

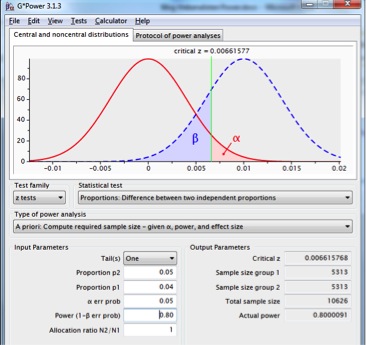
Voor de voorbeeld-case 4% vs 5% adviseert Gpower op basis van alpha=.05 en power=.80 twee steekproeven van 5.315:

Figuur 8: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04 (rode lijn) en p1=.04, p2=.05 (onderbroken blauwe lijn), met een betrouwbaarheid van .95, een power .80 en een eenzijdige test.

Deze benadering maakt gebruik gewenste betrouwbaarheid, verwacht effect en gewenste power in de berekening voor de benodigde steekproefomvang, en doet dat op basis van vuistregels; in die zin is er standaardisatie aangebracht.

Nu heeft de analist grip op de kans het verwachte/gewenste/benodigde effect in een test als significant op te sporen, namelijk .8.

Sommige online tools, bijvoorbeeld Visual Website Optimiser, maken gebruik van power in de steekproefgrootteberekening.

Visual Website Optimiser noemt in een presentatie een power van .8 een gebruikelijke maat.

Vraag is wel waarom dat een acceptabele regel is? Waarom zou de grootte van de power, evenals de omvang van de betrouwbaarheid niet dynamischer ingezet kunnen worden, of, als toch vuistregels gebruikt worden, waarom zou de analist die niet samen met de marketeer bepalen?

Oplossing ‘gewenste betrouwbaarheid en power’:

De analist zegt: split run met gewenste power en gewenste betrouwbaarheid bij een eenzijdige of tweezijdige toets.

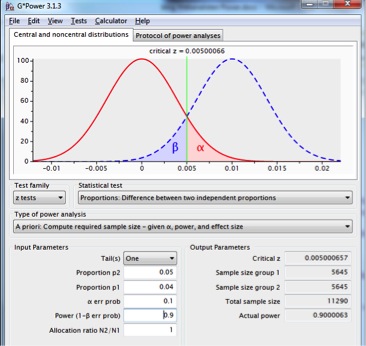
Volgt een discussie over acceptabele power en betrouwbaarheid met als conclusie, stel, beide 90%. Resultaat volgens GPower 2 keer 5.645 waarnemingen:

Figuur 9: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04 (rode lijn) en p1=.04, p2=.05 (onderbroken blauwe lijn), met een betrouwbaarheid van .90, een power van .90 en een eenzijdige test.

Wat als de marketeer zegt “dan duurt het te lang voor er voldoende waarnemingen zijn en is de landingspagina niet meer actueel. Er is ruimte voor gezamenlijk 3.000 testwaarnemingen en betrouwbaarheid is even belangrijk als power. De test wordt bij voorkeur wel uitgevoerd en een beslissing moet volgen”?

Resultaat op basis van deze beperking: betrouwbaarheid .75 en power .75.
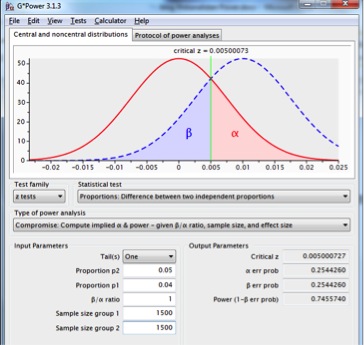
Als dit in orde is voor de betrokkenen, kan de test doorgaan op basis van alpha=.25.

Figuur 10: steekproevenverdeling voor het verschil tussen twee proporties met p1=p2=.04, n1=n2=1.500 (rode lijn), en p1=.04, p2=.05, n1=n2=1.500 (onderbroken blauwe lijn), waar betrouwbaarheid en power even groot zijn, met een eenzijdige test.

Deze benadering laat ruimte voor flexibele invulling van betrouwbaarheid en power. Ad hoc kan besloten worden voor diverse parameterinstellingen.

Nadeel is dat standaardisatie daarmee niet aanwezig is en tests onderling niet vergelijkbaar zijn.

Conclusie

Er zijn meerdere aanvliegroutes voor het berekenen van benodigde steekproefomvang, van twijfelachtige logica tot sterk onderbouwd.

Voorkeur van ondergetekende gaat uit naar de meest uitgebreide methode waarin zowel gewenste betrouwbaarheid als power worden betrokken in de berekening ‘gewenste betrouwbaarheid en power’. Is er geen peil te trekken op het verwachte effect, dan kunnen effectschattingen worden gemaakt in een pilot met “standaard steekproefomvang” of “standaard aantal conversies” en voor de vervolgtest de benodigde steekproefomvang worden berekend op basis van gewenste betrouwbaarheid, power en geschat effect.

Voor de vergelijkbaarheid tussen tests is het voor de jaarlijkse ‘mass’ aan tests handig vaste parameters voor betrouwbaarheid en power aan te houden. Voor crusiale ad hoc tests is het zinvol deze waarden naar wens bij te stellen.

Deze strategie op basis van gecalculeerd risico optimaliseert het percentage juiste beslissingen.